
Learn about torque: Force that causes an object to rotate around an axis. Introduction to Rotational Motion on Khan Academy.R ω / t r\omega/t r ω / t or r θ / t 2 r\theta/t^2 r θ / t 2 S / t S/t S / t or r θ / t r\theta/t r θ / t

Given S = r θ S = r\theta S = r θ and α = ω / t \alpha=\omega/t α = ω / t, therefore r α = r ω / t r\alpha=r\omega/t r α = r ω / t, which is the change in angular velocity over time. Essentially, "radians per second per second" or "radians per second squared".Īngular acceleration can be converted to tangential acceleration ( A t a n A_ A t a n ), which is acceleration which doesn't account for the change in direction in circular motion, by substituting arc length for angular displacement. Angular AccelerationĪngular acceleration ( α \alpha α) is the change in angular velocity over time, or α = Δ ω / Δ t \alpha=\Delta\omega/\Delta t α = Δ ω / Δ t. Given S = r θ S = r\theta S = r θ and ω = θ / t \omega = \theta/t ω = θ / t, therefore r ω = r θ / t r\omega = r\theta/ t r ω = r θ / t which equals S / t S/t S / t and S / t S/t S / t is distance over time, which is speed. Essentially, "radians per second".Īngular velocity can be converted to speed (note that speed is not the same as velocity) by substituting arc length for angular displacement. VariableĪngular velocity ( ω \omega ω) is the change in angular displacement over the change in time ( t t t), or ω = Δ θ / Δ t \omega = \Delta\theta/\Delta t ω = Δ θ / Δ t (again, the Δ \Delta Δ is often omitted). To be able to describe the factors affecting fluid mechanics.
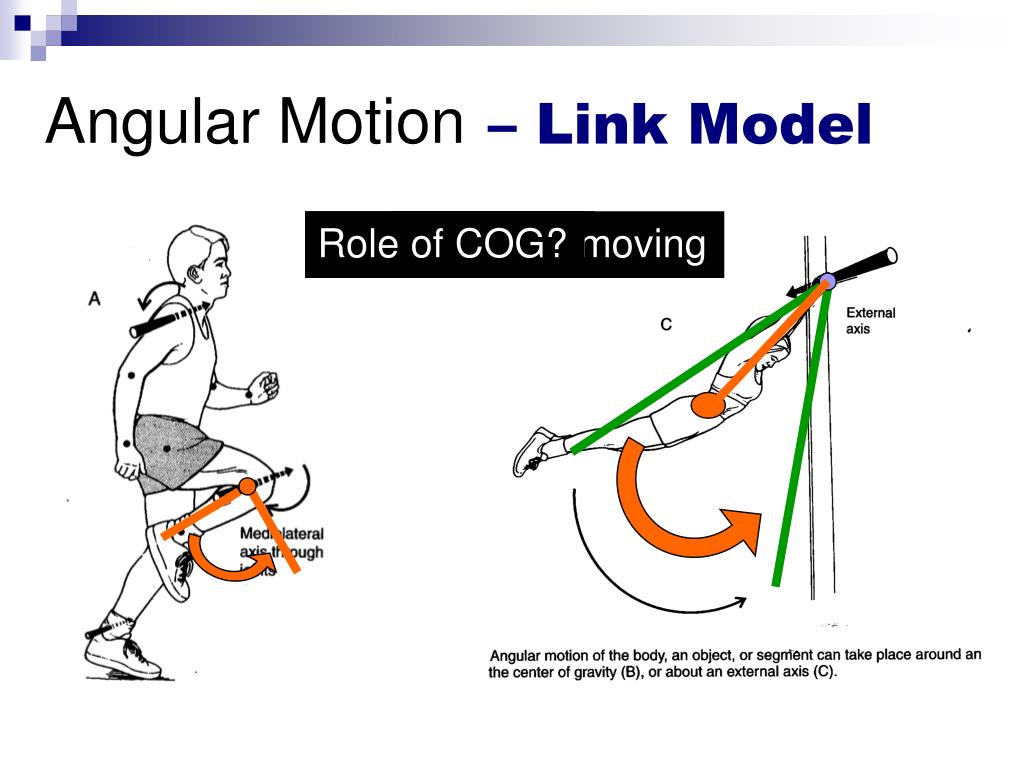
Angular displacement can therefore be calculated as θ = Δ S / r \theta = \Delta S/r θ = Δ S / r, though the Δ \Delta Δ is often omitted for brevity.Īngular displacement is the basis for angular motion because it allows all points on a rotating line to be measured, rather than just a single point by solving for the missing variable in the angular displacement calculation. To be able to explain the relationship between moment of inertia, angular velocity and momentum. The angular displacement of an arc length equal to the radius ( r r r) of a circle is, by definition, 1 r a d 1\ rad 1 r a d. Angular DisplacementĪngular displacement ( θ \theta θ) is the change ( Δ \Delta Δ) in angle in radians ( r a d rad r a d) of the arc length ( S S S) traveled by an object along a circular path. We will introduce a couple of additional concepts: torque (rotational analog of force) and rotational inertia (rotational analog of mass). By convention, measurements of angular motion are considered positive when the motion is counter-clockwise and negative when the motion is clockwise. When objects rotate, we will describe their motion with angular momentum (which could also be called 'rotational momentum'). Figure 11.1.1: Angular position for a particle moving around the z axis (out of the page.
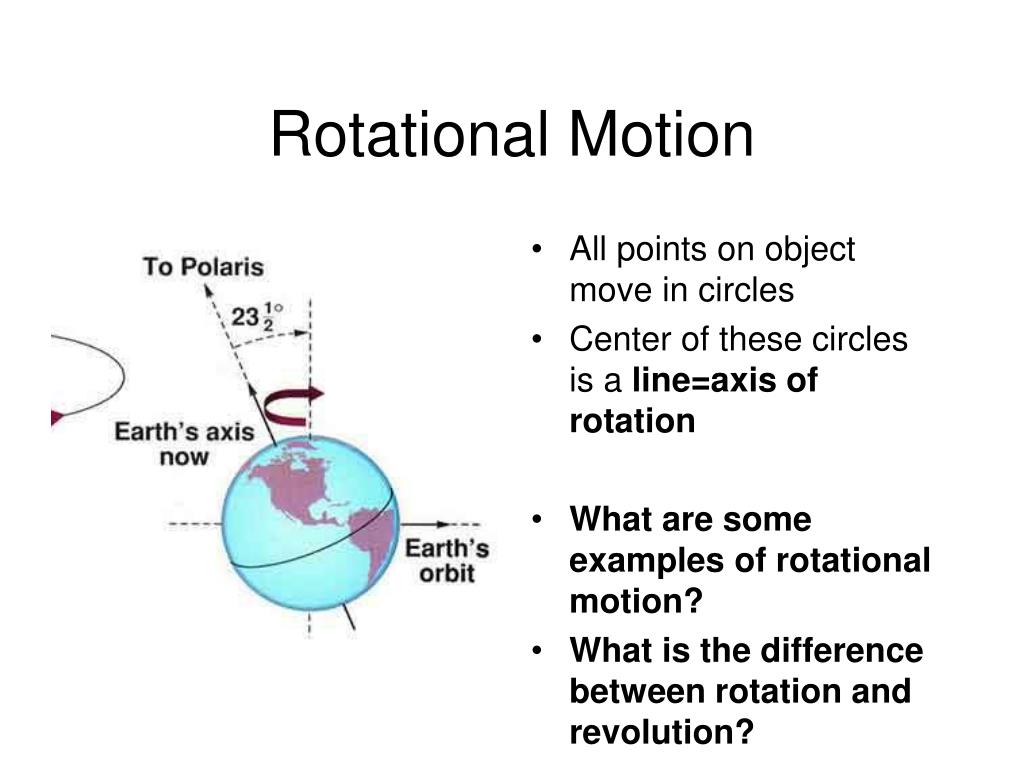
Angular motion is the motion of an object around a fixed axis point, such as a swinging pendulum or an orbiting planet. The angular motion is the motion where the body moves along the curved path at a constant and consistent angular velocity. With a suitable choice of coordinate system, the angular position can be defined as the angle made by the position vector of the particles, r, and the x axis of a coordinate system whose origin is the center of the circle, as shown in Figure 11.1.1.


 0 kommentar(er)
0 kommentar(er)
